みなさんは学生の頃、勉強は得意でしたか?
まぁ私は、得意な方でしたかね。たぶん。(たぶん。なのは自己申告なので、一応。笑)
さて、では自分の子供に勉強のコツを教えるとしたら、真っ先に思い浮かぶことがあります。(私が今まで実践していて、塾講師をしていたときにも生徒に伝えていたことです。)
今回は、そんな「お勉強のコツ」のお話。
覚えればよいことと理解すべきことを明確に区別する
それは、
「覚えればよいことと、理解すべきことを明確に区別して対応すること」
です。
具体例を挙げましょう。
例えば、歴史の勉強で覚える「関ヶ原の戦いは1600年に起こった」ということは、どちらにあたるでしょうか。
…これは、恐らく誰もが前者の「覚えればよいこと」に分類するでしょうね。
では次に、「27+35」は、どちらにあたるでしょうか?
…少し悩みましたか?でも、18+52の答えや、48-16の答えを、全部個別に暗記している人なんて居ないですよね。都度計算すれば答えは出せるので、それらの答えを個々に覚える必要はありません。これは、後者の「理解すべきこと」に分類されると考えられます。
ここで注目すべきは、「理解すべきこと」は、一度しっかりと理屈を頭に入れてやり方をマスターすれば、以降それらの問題に汎用的に対応できるようになる、という点です。言い換えれば、一つのやり方さえ身に付ければ、個別に対応する必要が無くなり、省力化できるということを意味しています。
このように、何か新しいことを学ぶときには、まずそれが「覚えればよいこと」なのか、「理解すべきこと」なのか、どちらなのかを判定し、前者であれば単に丸暗記、後者であればどうしてそうなっているのかの理屈・やり方をしっかり理解する、ということが重要になります。これを意識することで、効率良く学習を進めることができます。
両方の性質を持つもの
さて、では追加でもう一つご質問。
「6×9」は、どちらに分類されるでしょうか??
足し算が掛け算に変わっただけなので、さっきの足し算と同じく、後者の「理解すべきこと」でしょうか?でもちょっと待ってください。
みなさん、この答えは「ろっく、ごじゅうし」って丸暗記していますよね?
そう、お気付きの通り、一桁の掛け算は、”九九”というかたちで、「覚えるもの」として教えられます。しかし、本質的には、6を9個並べて、繰り返し足し算をし、その合計が結果として54になる、ということを理解しておかないといけません。ただし、一桁の掛け算は二桁以上の掛け算の基礎になるため、それらを計算する際に覚えていた方が早く、便利です。(毎回、数え直すのは面倒ですからね。)
こういった、本来は理解すべきことだが、その内容が広く応用でき、結果を覚えてしまった方が便利なものが存在します。公式や定理、法則と呼ばれるものが、主にそれにあたるでしょう。
これらを誤って「覚えればよいこと」だと勘違いし、理解せずに丸暗記をしてしまうと、その先には苦難が待ち受けています。その公式をちょっとひねった応用問題や、それらの理解を前提とした次の応用分野がさっぱり理解できなくなる、という事態に陥る可能性が高くなります。
こういった両方の性質を持つものについては、「あくまでも本来は理解しなければいけないことである」という認識を持ったうえで、「これは使い勝手が良いので、効率化のために結果も覚えておくとより便利だ」という意識でいることが重要になります。公式や定理は、基本的にやろうと思えば証明ができる程度までしっかり理解しておくべきでしょう。
| MEMO:よくある悪い例をひとつ。
例えば、X -1=5 を解くときに、「左辺のマイナス1を、右辺に持ってくるとプラス1に変わる」ので、X =5+1=6 とか覚えていませんか?まあ、中学校の先生はそう教えたかもしれませんね。 でも、そうではありませんよ。左辺の数を右辺に持ってくると、不思議なことになぜか符号がひっくり返る、というわけじゃないんです。ちょうど左辺の -1を打ち消すように、X -1=5 の左辺と右辺の両方に、+1 しているんです。 他にも似たような例は沢山ありますね。 |
以上のような内容をざっくりイメージにすると、こんな感じになります。
 Figure.2 学習対象の分類
Figure.2 学習対象の分類
さて、これらを区別して対応したほうがよいことがわかりました。
でも、一体どのようにして、覚えればよいことと理解すべきことを見分ければよいのでしょうか。これらを見分ける、妥当な判断基準はどのようなものでしょうか??
覚えればよいことと理解すべきことの見分け方
さて、何かを見分けるには、以前に汎化能力(→考える力の考察 その2「汎化能力」)で紹介した、「パターン認識」が役に立ちます。
ネコとチーターの見分け方では、体重と体長の2つを評価軸として選択しましたが、覚えればよいことと理解すべきことの見分け方での評価軸はたった一つ、「論理深度」であると考えます。
論理深度は、IBMの物理学者チャールズ・ベネットが提唱した、情報の価値をそのデータを生成するプログラムの計算量で測ろうとする概念ですが、ここでは厳密な定義は採用せず、単に文字通り、より深い論理の内部構造があるかどうか(ある物事について、何故そうなっているのかの”理由”であるとか、これを踏まえたうえでそうなっているなどの”前提”があるかどうか)と捉えます。
それ以上深い理由も前提も見当たらないような「単なる事実」は論理深度ゼロで、根拠や前提が幾層にも積み重なって成り立っている数学の公式などは、論理深度が大きい、と考えることができるということですね。そして、論理深度ゼロならそれがそのまま「覚えればよいこと」、論理深度が大きいほど、しっかり「理解すべきこと」と考えることができます。
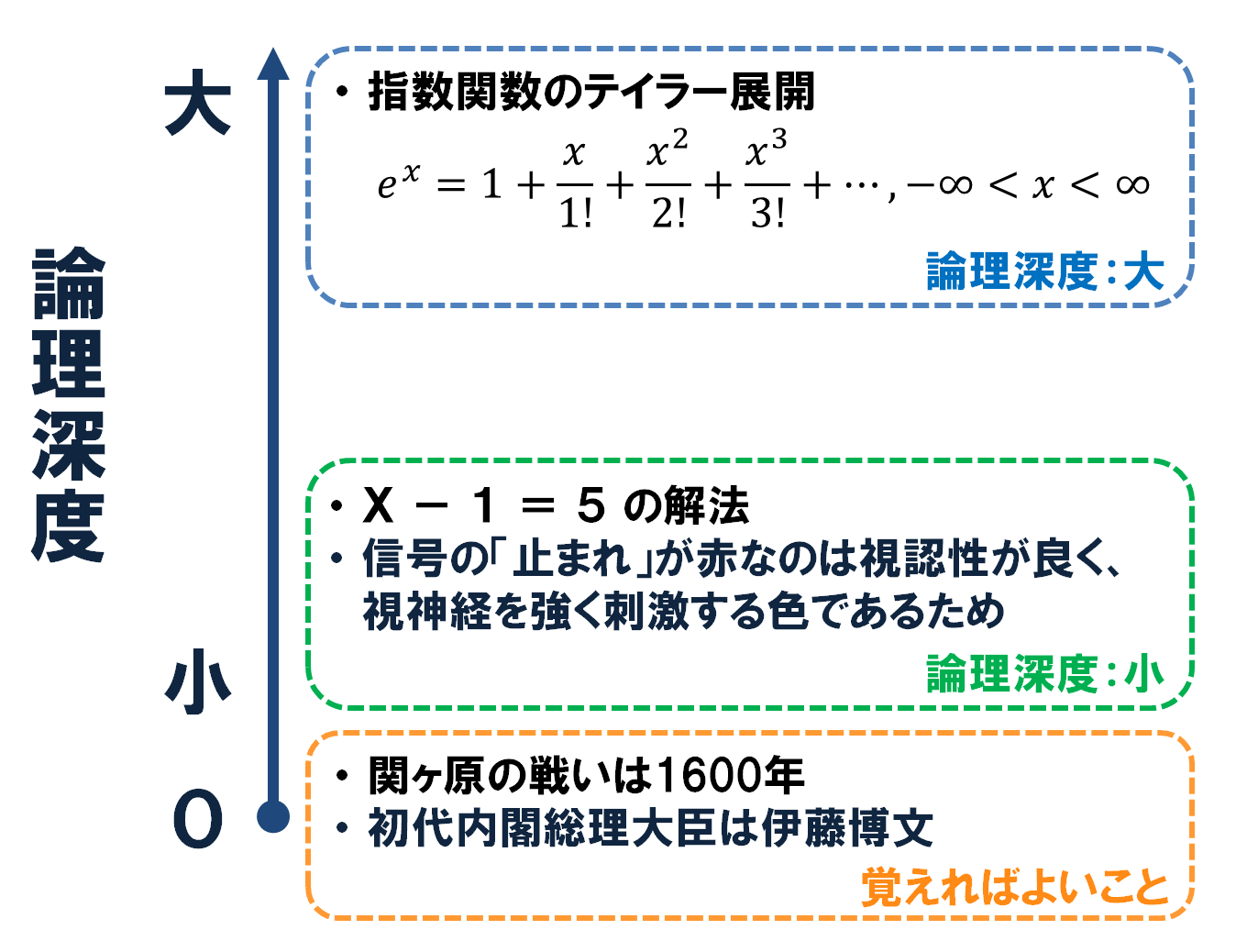 Figure.3 論理深度の例
Figure.3 論理深度の例
上述した例でいうと、「関ヶ原の戦いは1600年に起こった」という内容は、関ヶ原の戦いが、たまたま西暦が標準になった現代においてキリスト生誕から1600年後であったというだけで、その頃日本では西暦が使われていた訳でもなく、キリスト教と何か関連がある訳でもなく、それ以上の構造がない単なる事実であり、1600という数字になったのは単なる偶然であって何の意味もありません。従って、これは「論理深度がゼロ」であり、「覚えればよいこと」だと判断できます。
一方、「方程式を解くときに、左辺のマイナスを右辺に持ってくるとプラスに変わって解ける」という内容は、それ自体は自明ではなく、ユークリッド原論の公理の上に成り立っている方法ですから、こちらは「論理深度が1」と考えてよいでしょう。(ここでいう”1”という値は、論理や前提の”一段階”をどの程度の粒度で数えるかによって変わるので、あまり意味はありません。)こちらは、「理解すべきこと」だと分類するべきです。そして、理解したうえで、このやり方は広く汎用的に利用出来るので、やり方も覚えてしまった方が便利でしょう。
学校の勉強においては、概ね「論理深度がゼロか、それ以上か」だけでざっくり分けて、単純に覚えればいい科目はいつでも追い付けるので後回し、しっかり理解すべき科目(数学は明らかにこちらでしょう)は前もって時間をかけて理解を深めておく、というアプローチで問題ないと思います。くれぐれも注意しなければならないのは、定理や公式を丸暗記しないこと、つまり、「理解すべきこと」を「覚えればよいこと」だと取り違えないこと、「論理深度がゼロでない」ものを「論理深度がゼロである」ものと同じように対応しないことです。
今回のまとめ
- 覚えればよいことと理解すべきことを明確に区別すると効率よく学習できる。
- 両方の性質を持つものについては、何故そうなっているのかきちんと理解したうえで、結果も覚えるとよい。決して、理解せずに丸覚えしてはならない。
- これらを見分ける基準は、論理深度の大小。論理深度ゼロなら「覚えればよいこと」。論理深度が大きいほど、しっかり「理解すべきこと」。
ではでは今回はこの辺で。
この記事をいいね!と思ったら購読やシェアをしていただけるとうれしいです。


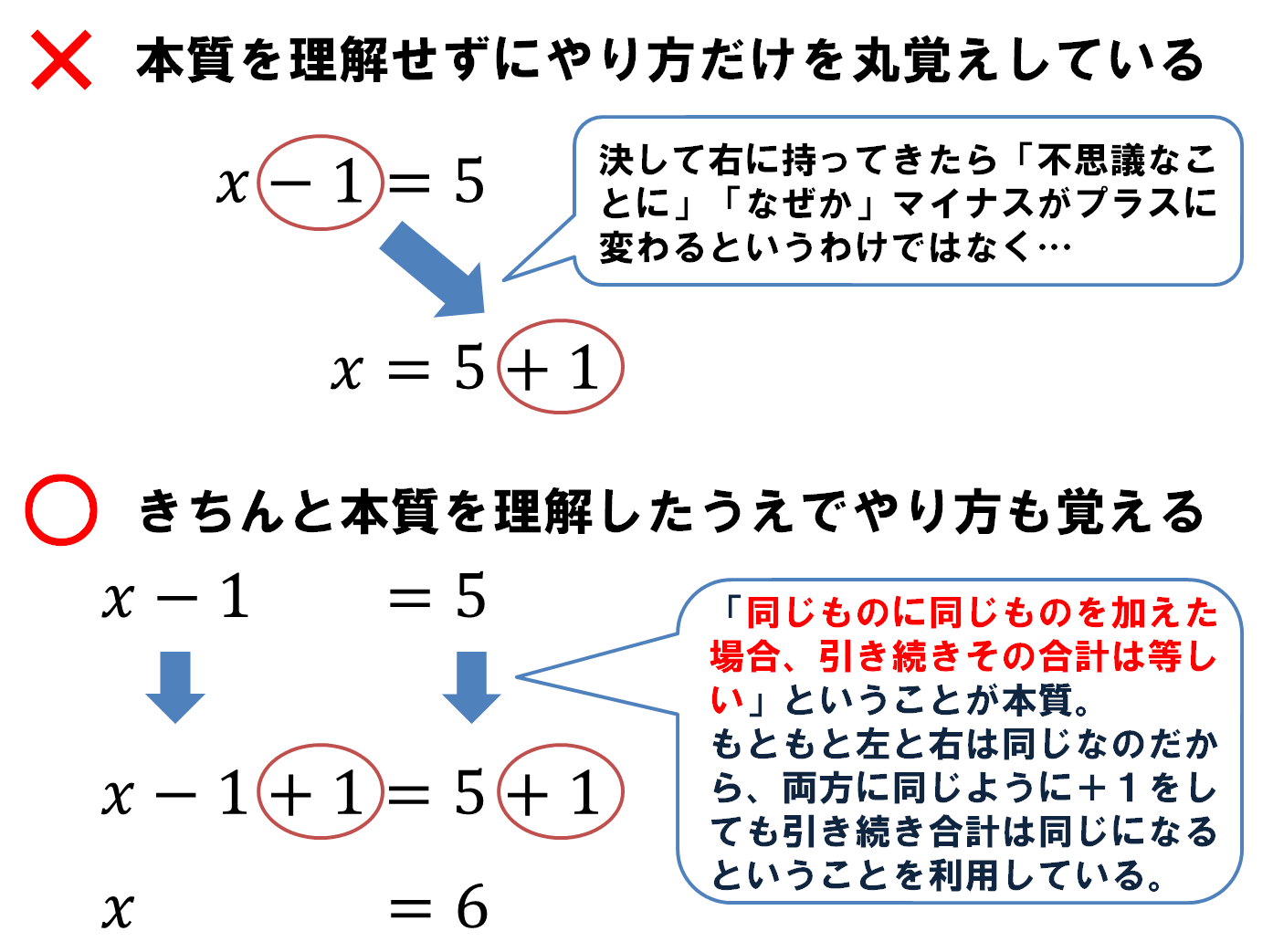 Figure.1 やり方だけを丸覚えしてしまった悪い例
Figure.1 やり方だけを丸覚えしてしまった悪い例















