今回は「お勉強のコツ」の話。の続編です。
さて、前回の「お勉強のコツ」の話。では、「覚えればよいことと、理解すべきことを明確に区別して対応すること」が重要であると説明しました。
このことはとても重要ですが、もちろん出来る工夫はそれだけではありません。勉強ができる人は、他にも幾つかのテクニックを使用して、勉強の効率化を図っていると考えられます。
その一つとして考えられるのが「単純化」です。今回はこれについて考察します。
「単純化」の対象と目的
まずはおさらいから。前回の図の再掲です。
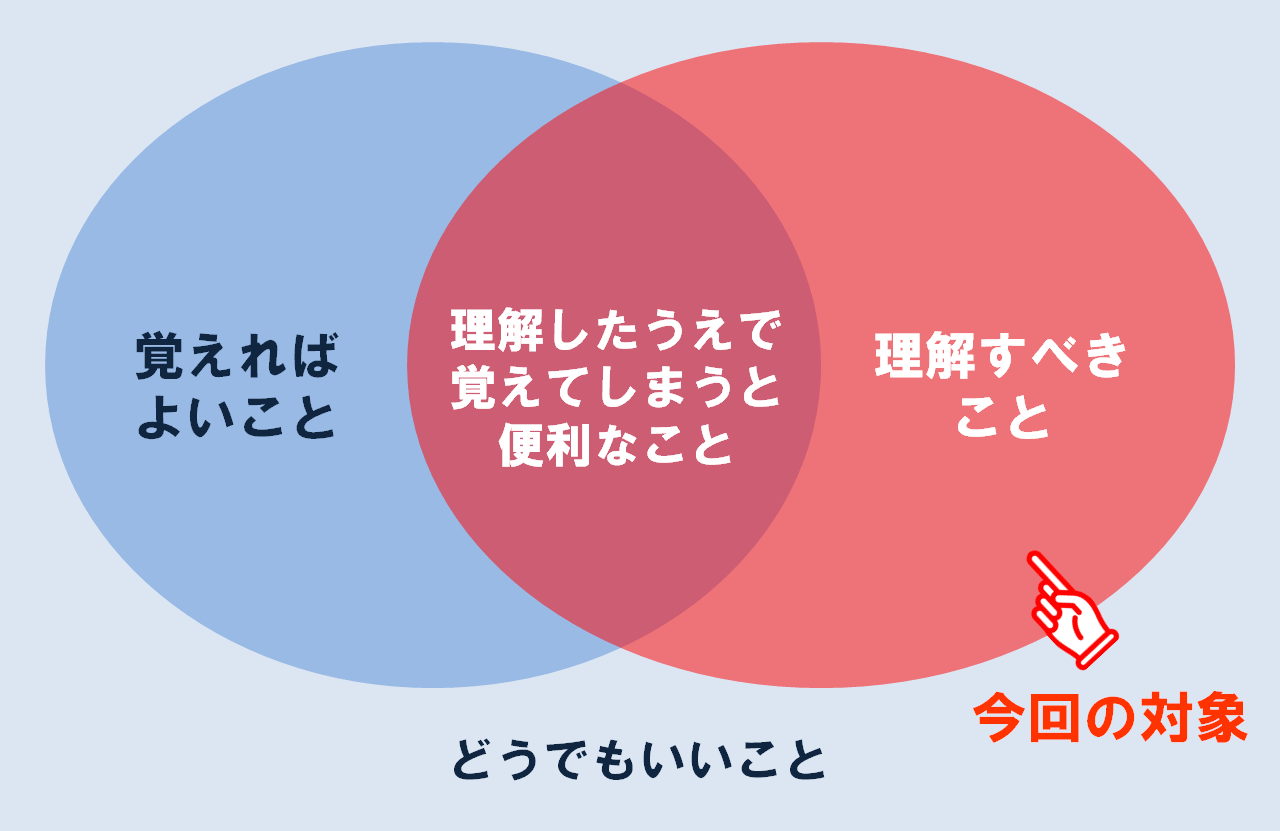Figure.1 「単純化」の対象
「単純化」の対象は「理解すべきこと」です。
学習の対象には、「覚えればよいことと」「理解すべきこと」、そしてそれらの両方の性質を持つ「理解したうえで覚えてしまうと便利なこと」がありました。今から学習しようとしていることが、どうやら「覚えればよいこと」ではなく、「理解すべきこと」のように思われる場合には、当然「しっかり理解する」ということが必要になります。
ところが、学習対象が複雑になればなるほど、「パッと見で」「直感的に」理解出来るものは少なくなっていきます。つまり、複雑な問題ほど、理解することが難しくなるということです（当たり前ですね！）。そのため、どうにかしてその複雑な問題を理解するために、何らかの工夫が必要になってきます。
そのときに有効なのが、「単純化」です。
「単純化」は、理解を助ける便利な思考ツール
頭の良い人は、複雑なものを複雑なまま理解しているように見えるかもしれませんが、実際にはそうではないように思います。むしろその逆で、頭の良い人ほど、複雑な問題をシンプルに捉えるのが上手いのではないでしょうか。
何か複雑な問題を考えるときには、いきなり複雑なまま考えようとしても、なかなか思考が前に進んでいきません。そこで思考の足掛かりとして、余計な要素を省いた極力単純なモデルを考えることで、思考を前に進めやすくします。単純なモデルで理解を深めたのち、徐々に複雑な場合を考えていくことで、最終的にはかなり複雑な問題にも対応することができるようになります。
「単純化」のテクニック
単純化には多くの場合に適用できるテクニックが幾つかあります。
以下では具体的な例を交えて、私がよく使う単純化の手法を３つご紹介します。
最も簡単な場合を考える
小学生で習う植木算を考えてみましょう。植木算とは、以下のような問題です。
概要
木を植える間隔や、植える木の本数、並木の長さなどを求める問題。問題が「木」でないこともよくある。例題1
42本の木が7m間隔で植えられている並木道がある。木は道の両側にあるとする。このとき、並木道の長さは何mか。
解法 冷静に考えれば難しくない問題である。
道路の片側にある木の数は、42÷2=21本。
21本の木にある「木の間」の数は20個（ここをしっかり考察することが、植木算の重要な点である）。
7×20=140、ゆえに140mが答である。
この問題を一般化すると、以下の公式になります。
公式
・一直線上に立っていて、両端にもある場合：木の本数＝木の間の数＋1
・一直線上に立っていて、両端にない場合：木の本数＝木の間の数－1
・円などの周りに立っている場合：木の本数＝木の間の数
これを用いて解く。
さて、では上記の公式を忘れてしまったときはどうすればよいでしょうか？そんなときでも、慌てることはありません。最も簡単な場合を考えてみれば、公式を考え出すことができます。
最も簡単な場合とは、これです。
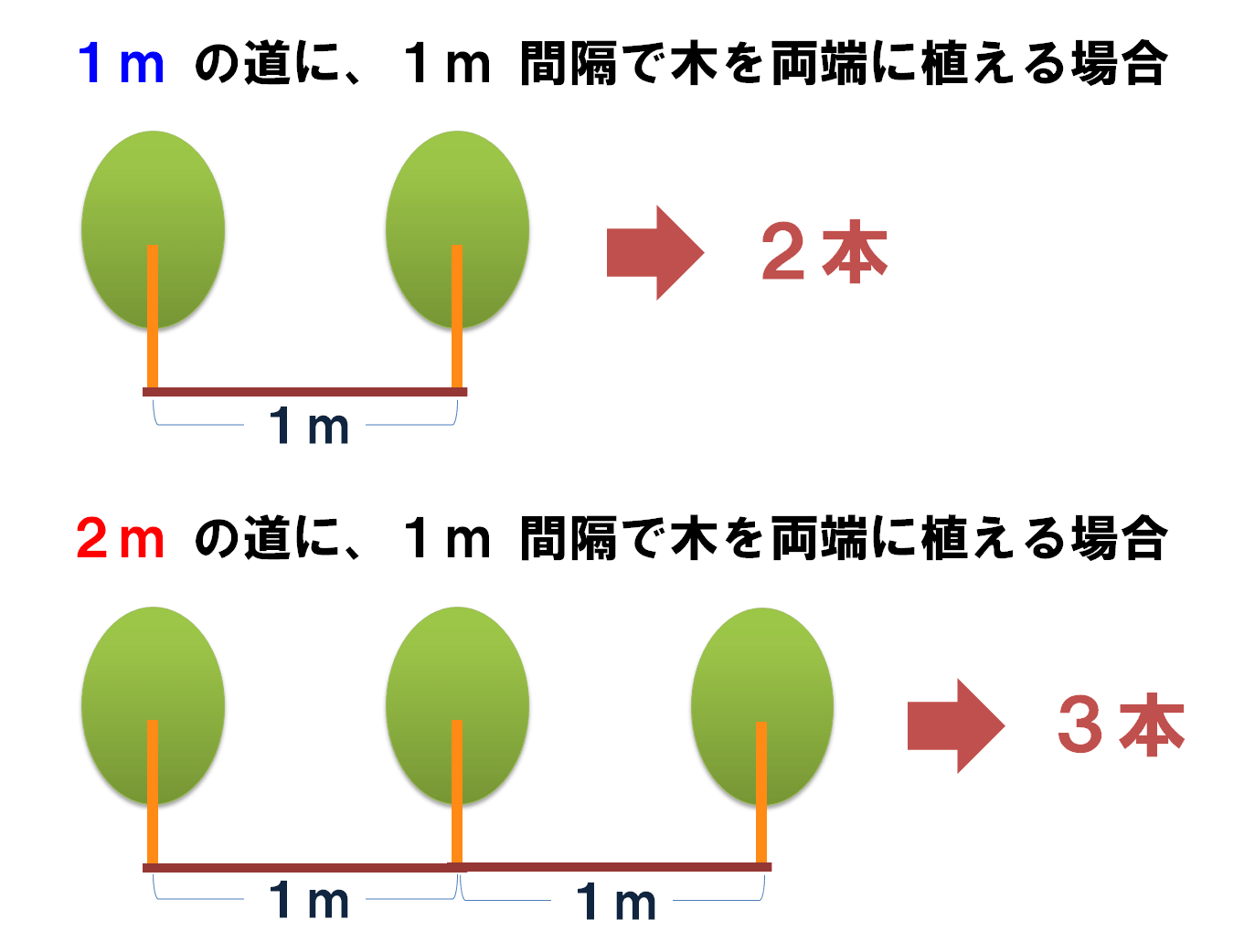Figure.2 植木算の「単純化」
1m の道に、1m おきに木を植える(両端にも植える)と、何本木が必要か？であれば、頭の中でもパッと想像できるでしょう。
最も簡単な場合が想像できたら、次は一つだけ増やしてみます。2m の場合です。これも、きっと頭の中で十分想像可能ですよね？
このように、最も簡単な場合を考え、少しずつ増やしていくことで、理解をしやすくすることができます。高校数学で出てくる漸化式、帰納法なども、これに近い考え方で一般化を行う手法であると考えられますね。
極端な場合を考える
二つ目の手法は「極端な場合を考える」です。以下の例題を考えてみましょう。
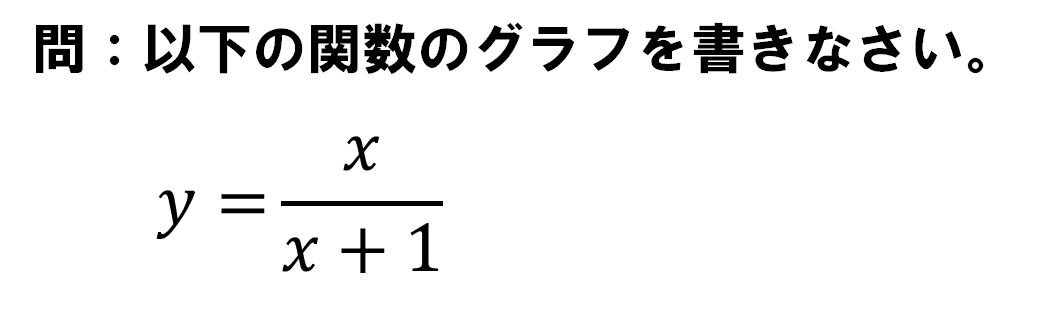Figure.3 関数グラフの形を予想する
あまり見慣れない形の関数で、パッと見でどんな形か瞬時に分かる人は少ないかと思います。こんなときには、とりあえずの取っ掛かりとして、極端な場合を考えてみましょう。X を「一億」にしてみます。すると、分母も分子も大体一億ですから、Y はほぼ１だろう、と推測することができます。X が「マイナス一億」でも同じで Y はほぼ１になりそうですね。厳密にグラフを描くには、式を変形するなど慎重に考察する必要がありますが、このように、取っ掛かりとして考えやすい場合で考え始めてみるのは有効です。
少し「極端な場合」とは異なりますが、「102 × 98」などを計算するときに、とりあえず 100 × 100 は一万だから、この答えも大体一万くらいになるだろう、とざっと見当をつけるのに応用することも出来ます。
変数を一つにしてみる
三つ目は、「変数を一つにしてみる」です。
人間の脳は、多くの要素を同時に増減させながらをその結果をリアルタイムでグリグリ動かしてシミュレーションするのは苦手です。上述したように、複雑なものを複雑なまま処理するのは難しいのです。このようなとき、思考を助けるために「変数を一つにする」という手法が役に立ちます。
ボールを投げて、一番飛距離が出る角度を求める問題を考えてみましょう。
Figure.4 ボールの斜方投射
この問題を、現実世界で厳密に考えるためには、ボールを投げる強さ、ボールの大きさや回転、空気抵抗、風の有無・方向、砲弾など長距離の場合は地球の丸みなども考える必要があるでしょう。しかしながら、これらをいきなり全部考慮して考え始めるのはあまりにも複雑で困難です。
そこで最初は、投げる強さは一定、ボールの大きさは考えず、回転も無し、空気抵抗ゼロ、風無し、地球の丸みなんて当然無視無視！！で考えてみます。
この単純化したモデルでは、変数は角度だけです。この場合には、簡単な計算で飛距離を算出することができ、一番飛距離が出るのは45度、という答えを導くことができます。
このように、まずは単純なモデルできっちり理解を深めるということが重要になります。
ここをしっかり押さえれば、これを足掛かりに、
- 次はボールの大きさを考慮し空気抵抗を一定と考える
- 次に風が吹いており空気抵抗が方向によって変わることを考える
- 更に、風の向きが変わり空気抵抗が方向だけでなく時間によって変わることを考える
- 更に…
といったように、思考を進めることが可能になります。
最初は単純なモデルを考え、徐々に要素を増やし、段階的に複雑な問題を考えていく、という手法は、この例がまさにそうであるように、物理学などでもよく使われるアプローチです。
「単純化」の効能
単純化を駆使して理解を助けることは、「なんだか難しくてよく分からない！もうやだ！勉強なんて嫌い！！」というような、「理解を投げ出さない」ためにも役立ちます。
長い時間をかけて勉強しているのに、なかなか理解できない、そんな状態が続くと、どうしても丸暗記をしたくなります。しかし、前回説明したように、それはその場しのぎであって、問題を先送りし、結果的に問題をより大きくするだけです。
単純化は、壁にぶつかったときに、一旦立ち止まり、足元を見て、一歩ずつ出来るところから歩を進めていく手段でもあると言えるでしょう。一歩ずつ考えを進め、問題が解けたときの喜びや達成感、すっきりとした晴れやかな気分、それを知ってもらうことで、勉強嫌いの一因も減らせるかもしれませんね。
今回のまとめ
- 複雑な問題ほど、理解するのが難しくなっていく。そのとき「単純化」が役に立つ。
- 人間は複雑なものを複雑なまま処理するのは苦手。複雑な要素を省いた極力単純なモデルを考えてみよう。
- 壁にぶつかったときでも、「理解すること」を投げ出さずに、一旦立ち止まって一歩ずつ考えを進めていこう。解けると気持ちいいよ。
ではでは今回はこの辺で。
この記事をいいね！と思ったら購読やシェアをしていただけるとうれしいです。
